Eine KI rekonstruiert das zweite newtonsche Gesetz und entdeckt eine bisher unbekannte Formel für die Masse-Berechnung dunkler Materie. Kann KI die Wissenschaft automatisieren?
Im Kern der Wissenschaft stehen zwei wesentliche Komponenten: Beobachtung und Logik. Erstere generiert Daten, aus denen wir dann mit Hilfe der Logik Regelmäßigkeiten erkennen und in der Sprache der Mathematik formulieren können.
Einmal formuliert, ist die mathematische Formel mehr als eine bloße Beschreibung der Daten – mit ihr können wir Vorhersagen treffen und bisher unbekannte Zusammenhänge entdecken.
Weshalb die Mathematik sich so hervorragend zur Formulierung von Naturgesetzen eignet, ist unklar. Diese Tatsache sei ein „wunderbares Geschenk, das wir weder verstehen noch verdienen“, schrieb der theoretische Physiker und Mathematiker Eugene Wigner in seinem Aufsatz „The Unreasonable Effectiveness of Mathematics in the Natural Sciences“.
Ohne das Zusammenspiel aus Daten und Mathematik wäre unsere Zivilisation nie entstanden. Doch je umfangreicher die Daten, je komplexer die Zusammenhänge, desto länger dauert üblicherweise die Entdeckung einer mathematischen Formel, die Regelmäßigkeiten in den Daten zutreffend beschreibt.
Wer im Matheunterricht eine lineare Funktion aus den Daten in einem zweidimensionalen Koordinatensystem ablesen soll, schafft das in fünf Minuten – oder schaut sich schnell ein Video auf YouTube an.
Bei komplexeren Aufgaben sieht das anders aus: Seit knapp hundert Jahren versuchen etwa Physiker Quantentheorie und Relativitätstheorie zu vereinen. Und wenn das gelingt, könnte es noch Generationen dauern, die Auswirkungen zu klären, meint etwa Physiker Lee Smolin.
Wenn KI wie Kolumbus ist, dann ist Rechenleistung die Santa Maria
Kann Künstliche Intelligenz die Entdeckung mathematischer Beschreibungen beschleunigen? Sollte es gelingen, Wissenschaft mit Rechenkraft zu automatisieren, könnte wissenschaftlicher Fortschritt an das mooresche Gesetz gebunden werden und so stark zunehmen.
Mit KI-Modellen lassen sich bereits jetzt komplexe Datenzusammenhänge modellieren und Vorhersagen treffen. Der Prozess ist im Kern einfach: Daten sammeln, KI trainieren und Vorhersagen treffen lassen. Das funktioniert für einen Gesichtsdetektor ebenso wie für eine KI, die die Bewegung von drei Körpern im Raum mit hoher Genauigkeit vorhersagen kann. Die KI lernt und entdeckt Zusammenhänge.
Doch die Blackbox neuronales Netz macht es fast unmöglich, zu verstehen, was sich im Inneren des Netzwerks abspielt. Und selbst wenn ein Einblick möglich wäre, ist die Repräsentation der gelernten Zusammenhänge in einem tiefen neuronalen Netz weit entfernt von den gesuchten mathematischen Beschreibungen.
Symbolische Regression produziert mathematische Beschreibung
Die Methode der symbolischen Regression kann das ändern. Mit ihr können aus den intern repräsentierten Zusammenhängen im Netzwerk mathematische Formeln abgeleitet werden.
Die symbolische Regression wird als genetischer Algorithmus ausgeführt. Ausgestattet mit Variablen und mathematischen Operatoren, sucht der Algorithmus nach der einfachsten mathematischen Formel, mit der sich ihm bekannte Daten reproduzieren lassen.
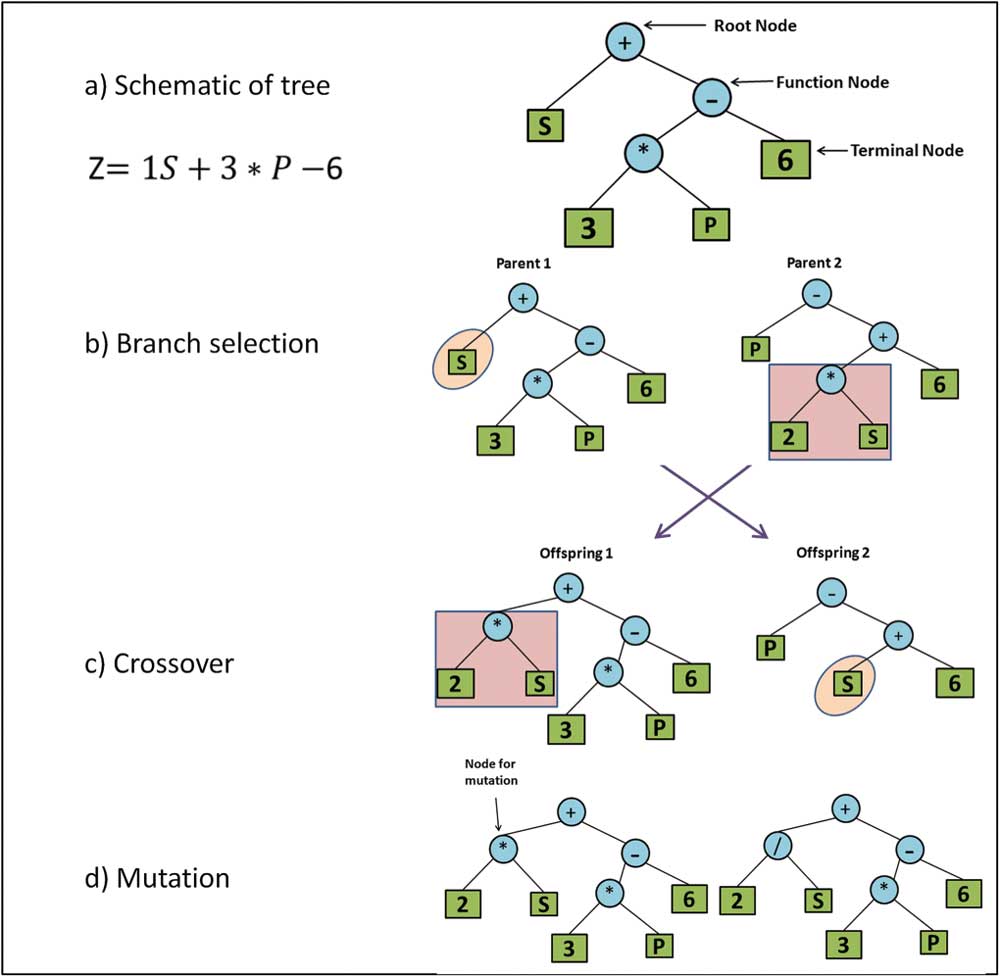
Dafür generiert er eine Vielzahl Formeln, vergleicht ihre Vorhersagen mit den bekannten Daten und übernimmt nur solche Formeln, die sich den echten Daten annähern. Die überlebenden Formeln werden dann modifiziert und erneut gegeneinander gemessen. Am Ende des Prozesses steht dann üblicherweise eine annähernd korrekte Reproduktion der vorhandenen Daten und eine einfache mathematische Formel.
Wer mehr über die Funktionsweise der symbolischen Regression wissen will, kann sich dieses Video über eine Implementation des Algorithmus in Python anschauen.
Von Grundgleichungen der Mechanik
Jetzt haben Forscher diese Methode genutzt, um die Bewegung von Teilchen und die Masseverteilung von dunkler Materie zu beschreiben. Dafür nutzen sie sogenannte neuronale Graphennetzwerke (GNN).
Diese neuronalen Netze setzen auf Graphen statt auf nacheinander angeordnete Schichten. Graphen bestehen aus mehreren Knoten (vertices), die miteinander verbunden sind (edges). Ein Knoten enthält Informationen, die über die Verbindungen an die Nachbarknoten weitergeben werden und so den Zustand des Empfängerpunktes verändern. So erhält jeder Knoten nach und nach Informationen über den gesamten Graphen.
Neuronale Graphennetzwerke eigenen sich besonders gut, um physikalische Systeme abzubilden, da diese häufig aus der Interaktion zwischen einzelnen Einheiten wie etwa Teilchen bestehen. Soll etwa die Bewegung mehrerer Teilchen vorhergesagt werden, speichern die Knoten Informationen zu den einzelnen Teilchen wie Koordinaten, letzte Bewegungsrichtung und Masse.
Ein Knotenpaar entspricht so zwei interagierenden Teilchen. Die Verbindungen enthalten Informationen über die Kräfte, die ausgehend von den Nachbarn auf die jeweiligen Teilchen (Knoten) wirken. Das gesamte System kann so die Beschleunigung einzelner Teilchen ableiten. Wird das GNN mit einem Datensatz entsprechender Teilchenbewegungen trainiert, wird seine Abbildung der Interaktion der Teilchen immer besser.
Die Forscher um PhD-Student Miles Cranmer haben jetzt ein GNN trainiert und mit der symbolischen Regression die Grundgleichung der Mechanik – Kraft ist Masse mal Beschleunigung – aus dem Netzwerk abgeleitet.
Ihr Resultat zeigt deutlich, dass die Mischung aus Daten, neuronalen Graphennetzwerken und symbolischer Regression tatsächlich geeignet ist, um mathematische Formeln – in diesem Fall ein bereits bekanntes Naturgesetz – aus Daten mit KI zu gewinnen.
Dunkle Materie mit KI berechnen
Angespornt von diesem Erfolg, wandten sich Cranmer und Kollegen einem aktuellen Forschungsbereich der Kosmologie zu: Sie wollten eine bestimmte kosmologische Eigenschaft (übermäßige Dichte) einer Ansammlung dunkler Materie abhängig von den Eigenschaften anderer Ansammlungen dunkler Materie in ihrer Umgebung berechnen.
Dunkle Materie macht circa 85 Prozent aller Materie des Universums aus, sammelt sich in riesigen Strukturen und bildet so Gravitationsbecken, sogenannte Dunkle-Materie-Halos. In diesen Becken sammelt sich die sichtbare Materie und formt Sterne und Galaxien.
Die Forscher griffen erneut auf das neuronale Graphennetzwerk zurück. Jeder Knoten enthält Informationen über einen Dunkle-Materie-Halo wie Position, Geschwindigkeit und Masse und ist mit anderen Halos in einer Entfernung von 50 Mpc/h verbunden. Trainiert wurde das Netzwerk mit Daten der Quijote Dark Matter Simulation, einer Sammlung generierter Dunkle-Materie-Strukturen.
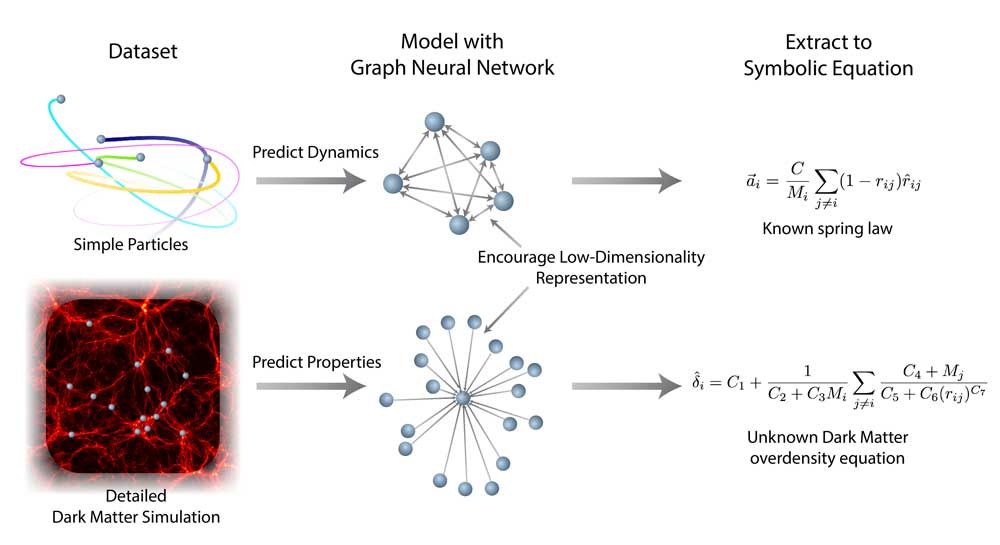
Nach dem Training konnte das GNN die gesuchte Eigenschaft der Halos genauer als bisherige Modelle vorhersagen. Mit der symbolischen Regression konnten die Forscher anschließend eine bisher unbekannte mathematische Formel produzieren, die eine geringere Fehlerrate als die aktuell meistgenutzte menschengemachte Formel für die gleiche Aufgabe hat.
Die so entstandene Formel konnte außerdem besser mit bisher unbekannten Daten umgehen. Für Cranmer ist das ein klares Zeichen, dass die mathematische Formel wesentlich besser generalisiert als das neuronale Graphennetzwerk, aus dem sie gewonnen wurde. Das decke sich mit unserer bisherigen Erfahrung in der Physik, so Cranmer: „Die Sprache einfacher symbolischer Modelle beschreibt das Universum zutreffend.“
Die Erfolge von Cranmer und seinen Kollegen zeigen, dass der Einsatz von KI in der Forschung zur Entdeckung bisher unbekannter Formeln führen kann. Das würde die Arbeit von theoretischen Physikern erleichtern. Doch die Entdeckung selbst ist nur der erste Schritt, anschließend müssen die neuen Formeln mit bekannten vereint und abgeleitet werden. Und da müssen – vorerst – noch Menschen ran.